During one of my lectures, I began to question the assumption that computers can only understand 1s and 0s. Lecturers tell us our applications and protocols must work only in binary. We, the latest generation of computer scientists, are slowly being brainwashed into worshipping the binary form, and we rise up in anger at the blasphemous rantings of anybody exploring the possibility of an alternative.
Computers have been around since the 1940s and binary has long been the computing industry standard. Binary is fantastic, a simple solution to the problem of data transfer between and within computers. But it also has its limitations. Consider a piece of data 2 bits long. Assuming a bit can only be 1 or 0, there are a total of four possible combinations of bits; 00, 01, 10, or 11. If we could choose another bit, which we shall call 2, we would have 9 possible combinations (00, 01, 10, 11, 02, 20, 21, 22, 12).
The number of bits in our data has an impact on hard drive space, network bandwith, and processing time. We should be considering all options to reduce the impact data length has on these things- trinary would dramatically reduce the problem.
UNIX timestamps (used across the world wide web and in many software systems) represent time as the number of seconds since the 1st of January, 1970. The time in seconds elapsed since that date is stored in a 32-bit integer, and, in binary, this means that the timestamp can only hold time up until 03:14:07 UTC on Tuesday, 19th January 2038. This is because 32 bits can store up to 2^32 seconds, which equates to 4,294,967,296 seconds. And that equates to just over 68 years.
The 2038 problem won’t be a problem for over 25 years, but in computing, we should make sure our systems are stable and have longevity. The proposed solution to the 2038 problem is using a 64-bit int, which would not overrun until Sunday, 4th December 292,277,026,596. As this is over 20 times the theorised age of the universe, we wouldn’t have to worry about running out of space anytime soon. But this also means using twice as much space to hold exactly the same information.
Storing seconds in a 32-bit TRINARY int would give 3^32 seconds, giving 1,853,020,188,851,841 seconds since January 1st, 1970. This equates to over 58,758,884 years- which is still a pretty good long term system! Coming up with a trinary solution would reduce or remove countless problems in computing. Applications would run faster, data would take up much less space on hard drives, download speeds would be quicker (not only due to smaller file sizes, but as a result of a new Internet Protocol with smaller IP Headers). Rather than coming up with new and better ways of storing and transporting binary data, perhaps we should look into inventing trinary?
With this thought in mind, I got working on trinary the moment I got back from my lecture. The first thought I came up with:
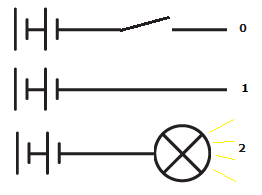
As you can see, when the switch is open, nothing is being sent, which could be considered a binary 0. When the switch is closed, a current passes down the wire, which could be interpreted as a binary 1. You can either have electricity, or not- what I was trying to come up with was something in between. And my initial thought was light. Electricity could power a bulb or LED of some sort, which would be picked up by a sensor on another circuit, which would treat the signal as a trinary “2”.
I wasn’t hopeful about this idea, so I continued scribbling down my thoughts, and came up with a second concept:
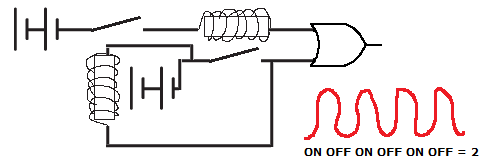
This is a little more tricky. Electricity is passed down the wire and goes through an electromagnetic coil. It passes through this coil and into a logical OR gate, coming through as a binary 1. However, a magnetic field is created, forcing down a second switch in the circuit. This second switch allows another current to flow through to the OR gate, which is still treating this as a 1. Eventually, the current flows through a second electromagnetic coil, which pushes open the original switch, cutting off the original current. This kills off the original magnetic field, meaning the second switch opens and no current flows anymore. At this point, no current is coming from the OR gate, so this could be a binary 0.
Okay, so I didn’t think the design through properly, but the idea is that electricity flows and stops and flows and stops and flows through the OR gate thousands of times per second. This constant fluctuation in current could be considered a trinary 2, provided there is some intelligence in the circuit.
Again, I didn’t hold high hopes for the idea, so I kept thinking.
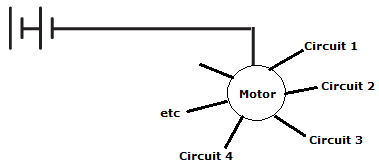
The basic principle behind this idea was that some sort of motor could rotate and change which circuit to send a current down. There could theoretically be an unlimited number of potential circuits to connect to, but let’s say there were 8. Hey presto, I’ve just invented octary! Depending on which circuit the current flows through, that could represent an octary 0, 1, 2, 3, 4, etc.
Of all the weird and wonderful ideas, this was the least likely to work. So I had another go.
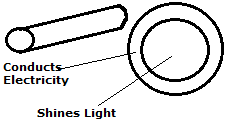
Let’s imagine we have a hollow cable- this can be metal, synthetic, whatever, but it has to conduct electricity. Let us also imagine we can send light down this cable. Suddenly, we have more options than even trinary can possess.
No electric signal, no light. OUTCOME = 0
Electric signal, but no light. OUTCOME = 1
No electric signal, but we do have light. OUTCOME = 2
Both electric and light signal. OUTCOME = 3
Theoretically, if we can perfect this type of technology, we could have four different bit types.
Satisfied with my work, I went to bed, before I realised I’d skipped a fundamental step- checking trinary on Google! Alas, somebody has beaten me to it. In the late 1950s, Nikolay Brusentsov produced the Setun- the only modern, electronic trinary (or ternary) computer. It had a lower electricity consumption and lower production cost than the binary computers that replaced it.
According to computer-museum.ru, “Setun has an one-address architecture with one index-register. The contents of it, in dependence of value (+,0,-) of address modification trit, may be added to or subtracted from the address part of instruction. The instruction set consists only of 24 instructions including performing mantissa normalization for floating-point calculation, shift, combined multiplication and addition. Three instructions are reserved but have never been used because of the lack of necessity.”
“Simplicity, economy and elegance of computer architecture are the direct and practically very important consequence of the ternarity, more exactly – of representation of data and instructions by symmetrical (balanced) code, i.e. by code with digits 0, +1, -1. In opposite to binary code there is no difference between “signed” and “unsigned” number. As a result the amount of conditional instructions is decrease twice and it is possible to use them more easily; the arithmetic operations allow free variation of the length of operands and may be executed with different lengths; the ideal rounding is achieved simply by truncation, i.e. the truncation coincides with the rounding and there is the best approximation the rounding number by rounded.”
Here is another quote I found interesting: “In ‘Setun 70’ the peculiarities of ternarity are embodied with more understanding and completeness: the ternary format for symbols encoding – “tryte” (analog of binary byte) consisting of 6 trits (~9.5 bits) is established; the instruction set is updated of auxiliary ternary logic and control instructions; arithmetic instructions now allow more variation of operand length – 1, 2 and 3 trytes and length of result may be up to 6 trytes.”
It appears trinary already exists. So why did it fail?
There seems to be no reason other than the increasing popularity of binary at the time. Binary components were already being mass produced, and officials of the computer production in the USSR disapproved of the unplanned and unusual proposal of trinary as an alternative to existing systems. The cost, financially and in terms of time lost, of replacing all existing computing technology in favour of trinary systems was simply too high.
The future for trinary is uncertain, but Donald Knuth, author of “The Art of Programming”, predicts trinary’s return, due to its elegance and efficiency. A possible modern trinary solution could be to use fiber optics, where dark is 0 and the two orthogonal polarizations of light are 1 and -1.
I can’t help feeling that if it were feasible for the world’s computing industry to use trinary, it would be using it by now. And if the cost and time taken to replace the world’s computers and networks seemed daunting back in 1960, imagine the mammoth task we are presented with today! In the same way that the internet was built on top of existing technologies (read: 4kHz telephone cables), I think we’re stuck with what we’ve got for a good couple of decades. New, state-of-the-art systems are continually being built, and those systems may soon be being built on a trinary foundation. The rest of the world then needs to catch up, and that will take some time.